Skip to main content

📐 Geometry Distance

Different methods to measure distance between two data points.

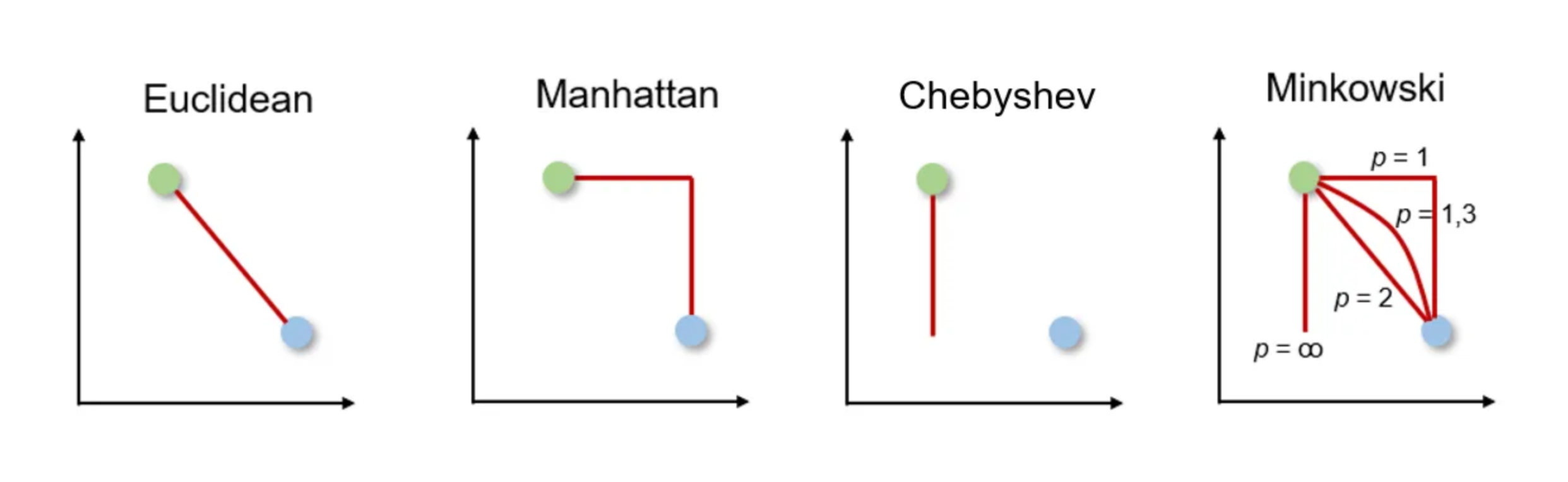
Illustration comparing four distance metrics: Euclidean uses straight-line distance, Manhattan follows horizontal and vertical paths, Chebyshev takes the maximum of horizontal and vertical distances, Minkowski varies with different p values

Source

Euclidean​

Straight-line distance (good for physical space).

DEuclidean(p,q)=∑i=1n(pi−qi)2D_{\text{Euclidean}}(\mathbf{p}, \mathbf{q}) = \sqrt{ \sum_{i=1}^{n} (p_i - q_i)^2 }

Manhattan​

Grid-based movement (like walking city blocks).

DManhattan(p,q)=∑i=1n∣pi−qi∣D_{\text{Manhattan}}(\mathbf{p}, \mathbf{q}) = \sum_{i=1}^{n} |p_i - q_i|

Chebyshev​

maximum difference along any coordinate dimension between two vectors.

DChebyshev(p,q)=max⁡i=1n∣pi−qi∣D_{\text{Chebyshev}}(\mathbf{p}, \mathbf{q}) = \max_{i=1}^{n} |p_i - q_i|

Minkowski​

Generalization of all the above.

  • p=1p = 1 is Manhattan
  • p=2p = 2 is Euclidean
  • p≈inf⁡p \approx \inf is Chebyshev
DMinkowski(p,q)=(∑i=1n∣pi−qi∣p)1pD_{\text{Minkowski}}(\mathbf{p}, \mathbf{q}) = \left( \sum_{i=1}^{n} |p_i - q_i|^p \right)^{\frac{1}{p}}